This software helps to solve "gratte-ciel" puzzles as they can be found in the french magazine "tangente jeux" (very interesting puzzles IMHO). Two original puzzles are given, but first let's introduce the principle of the game:

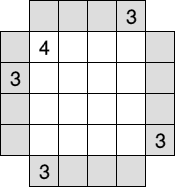
A city block has been represented in the grid. Each square contains a skyscraper of height 10;20;30 or 40 meters (abbreviated here to 1;2;3 or 4). Buildings in the same row or the same column all have differents heights. Moreover the informations given in the gray squares surrounding the city block indicate the number of visible buildings from this point of view. For example if a row contains 2-4-3-1 then two buildings are visible from the left and three are visible from the right. Your goal is to find the height of each skyscraper.

Now to use the software for solving the puzzle (try it first by hand if you are not used to it!), you must create a text file called "free.gc" and containing the following text:

4        size
...3     up
3...     down
.3..     left
...3     right
...4 1234 1234 1234     possibilities for each position
1234 1234 1234 1234
1234 1234 1234 1234
1234 1234 1234 1234

On the first line is the size S, between 1 and 9. The following four lines contain S values which are the number of skyscrapers visible from the current position. If no value was given in the magazine, just put a dot instead of a digit (so you must always have S characters). Then you have S lines containing S blocks of S possibilities. If a height is impossible, you just put a dot instead of the value. Since the upper left skyscraper has a height of 4 then the values 1;2 and 3 are impossible, thus it is encoded "...4".

Now let's give the file to the program by typing "gciel free.gc >free2.gc" under the do$ prompt (or "gciel free/gc { > free2/gc }" on RiscOS). You now have a file called "free2.gc" which contains the entry file followed by the solution:

4 size
...3 up
3... down
.3.. left
...3 right
...4 ..3. 1... .2..
1... .2.. ...4 ..3.
..3. 1... .2.. ...4
.2.. ...4 ..3. 1...

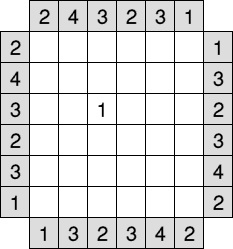In the puzzle aside skyscrapers can have a height of 10;20;30;40;50 or 60 meters (abbreviated as 1;2;3;4;5 or 6). It has a blind area in the middle (it can't be seen from the edges), but alas even without this feature this grid has multiple solutions. I added a value in the center so as to reduce the number of possibilities.

Like some others, this puzzle cannot be solved by the program only. Once you give the entry file to the program, it reduces the number of possibilities, as you can see below:

6 size
243231 up
132342 down
243231 left
132342 right
....5. 123... .234.. 1234.. 1234.. .....6
123... .234.. ..3.5. .....6 .2345. 1234..
.234.. ..3.5. 1..... .2345. .....6 .234..
1234.. .....6 .2345. 12345. ..3.5. 1234..
1234.. .2345. .....6 ..3.5. .234.. 123...
.....6 1234.. .234.. 1234.. 123... ....5.

So now you can make some tests. Choose a square with only a few values, for example the (x=2;y=3) square, and try to set it to "..3..." instead of "..3.5.". As you will dicover the solver returns a crappy solution, thus the correct value is "....5.", so set it. Then go on like this until you have a valid solution.